Σκοπός αυτής της διπλωματικής εργασίας είναι η μελέτη της αποδοτικότητας της μεθόδου ισογεωμετρικής ανάλυσης όταν συνδυάζεται με πλαστική ανάλυση με το υστερητικό μοντέλο Bouc – Wen. Τρία είναι τα κύρια μέρη που απαρτίζουν την εργασία. Το πρώτο μέρος, περιέχει την παρουσίαση των μεθόδων στην υπολογιστική γεωμετρία, το δεύτερο τη μέθοδο ισογεωμετρικής ανάλυσης και το τρίτο τον συνδυασμό του υστερητικού μοντέλου με την ισογεωμετρική ανάλυση.

Στο πρώτο μέρος, κατασκευάζονται σταδιακά τα NURBS. Πρώτα, σημειώνεται πόσο σημαντικές είναι οι μέθοδοι της παρεμβολής και της προσέγγισης στα γραφικά υπολογιστών και την υπολογιστική γεωμετρία. Επιπλέον, τονίζεται η διαφορά μεταξύ των δύο μεθόδων· προς αυτήν την κατεύθυνση, παρατίθενται μερικές καμπύλες παρεμβολής και μερικές προσέγγισης. Η παρουσίαση των τελευταίων καμπυλών ξεκινά με τα πολυώνυμα Bernstein, τα οποία αποτελούν βάση για την κατασκευή των καμπυλών Bézier (ρητών ή μη). Ενώνοντας δύο ή περισσότερες τέτοιες καμπύλες προκύπτει μία καμπύλη B-Spline (ρητή ή μη, αντίστοιχα). Ταυτόχρονα με την μελέτη των μεθόδων κατασκευής όλων αυτών των καμπυλών προσέγγισης, αναπτύχθηκαν κώδικες στη Matlab που υπολογίζουν και εκτυπώνουν καμπύλες, επιφάνειες και στερεά, καθώς και την κ-οστη ( 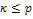, όπου p είναι η τάξη της πολυωνυμικής συνάρτησης) παράγωγο σε οποιοδήποτε σημείο του πεδίου ορισμού. Συνεπώς, κάνοντας ένα βήμα τη φορά, επετεύχθη η κατασκευή μιας βιβλιοθήκης από κώδικες Matlab για κατασκευή και εκτύπωση των συναρτήσεων βάσης B-Splines (ρητών NURBS και μη ρητών) και των αντίστοιχων γεωμετριών.

Στο δεύτερο μέρος, παρατίθενται στον αναγνώστη σημαντικά μέρη από το μαθηματικό υπόβαθρο και τη θεωρία των πεπερασμένων στοιχείων. Στη συνέχεια, γίνεται μια προσπάθεια σύνδεσης της θεωρίας των πεπερασμένων στοιχείων με τις γεωμετρικές συναρτήσεις βάσης. Έπειτα, σχολιάζεται ένα πλήθος από διαφορές που εμφανίζουν οι γεωμετρικές και οι συμβατικές συναρτήσεις βάσης στη μέθοδο των πεπερασμένων στοιχείων. Στη συνέχεια, κατασκευάζουμε τα κινηματικά μητρώα για το πρόβλημα επίπεδης έντασης και παρουσιάζουμε δύο παραδείγματα γραμμικών προβλημάτων επίπεδης έντασης. Ακόμα, διερευνήθηκε η μέθοδος αριθμητικής ολοκλήρωσης με πολυώνυμα Legendre των γεωμετρικών συναρτήσεων βάσης. Τέλος, έγιναν παραμετρικές αναλύσεις με πύκνωση της διακριτοποίησης και αύξηση του βαθμού συνέχειας των γεωμετρικών συναρτήσεων σχήματος, ώστε να εξακριβώσουμε την ορθότητα του κώδικα που αναπτύξαμε.

Στο τελευταίο μέρος της εργασίας αυτής η ισογεωμετρική ανάλυση συνδυάζεται με το υστερητικό μοντέλο Bouc – Wen. Ο αναγνώστης μπορεί να ενημερωθεί για το φαινόμενο της υστέρησης από την εισαγωγή. Στη συνέχεια ακολουθούν αποσπάσματα της διδακτορική διατριβής του Τριανταφύλλου Σάββα για την μαθηματική μοντελοποίηση του μοντέλου υστέρησης Bouc-Wen σε επίπεδο δυνάμεων και στον πλήρες χώρο των τάσεων. Ακολούθως γίνεται η τεκμηρίωση της νομιμότητας της εφαρμογής του γενικευμένου υστερητικού μοντέλου Bouc-Wen στην ισογεωμετρική ανάλυση. Αναπτύσσονται τα βασικά μητρώα για μια τέτοια ανάλυση και παρουσιάζονται εφαρμογές σε μονοτονική και ανακυκλιζόμενη φόρτιση. Στο τέλος, γίνονται παραμετρικές διερευνήσεις για την απόδοση της μεθόδου και εξάγονται συμπεράσματα.