Ο σκοπός της παρούσας μεταπτυχιακής εργασίας είναι η ανάπτυξη αλγορίθμου για τη διερεύνηση της μηχανικής συμπεριφοράς υλικών με χρήση της μοριακής δυναμικής. Η μοριακή δυναμική μας βοηθάει να αναλύσουμε το υλικό σε μικροσκοπική κλίμακα, δηλαδή σε επίπεδο μορίου και να αποφανθούμε για κάποιους από τους πιο θεμελιώδεις μηχανισμούς του κυρίως στη πλαστική περιοχή.

Δηλαδή είναι μια υπολογιστική μέθοδος όπου η χρονική εξέλιξη ενός συστήματος ατόμων που αλληλεπιδρούν καθορίζεται από την ολοκλήρωση των εξισώσεων κινήσεως τους, ορίζοντας αρχικές συνθήκες (θέσεις, ταχύτητες επιταχύνσεις) σε όλα τα άτομα του συστήματος, κατάλληλο στατιστικό σύνολο καθώς επίσης και τη συνάρτηση δυναμικού που περιγράφει την αλληλεπίδραση μεταξύ τους. Αποτελούν ένα σημαντικό εργαλείο για τη μελέτη των μακροσκοπικών ιδιοτήτων ενός υλικού εξετάζοντας τους μοριακούς μηχανισμούς που διέπουν τη συμπεριφορά τους, συνδέοντας έτσι το μικρόκοσμο με το μακρόκοσμο.

Στα πρώτα κεφάλαια παρουσιάζεται ο αλγόριθμος μοριακής δυναμικής χωριζόμενος σε τρία μέρη, την αρχικοποίηση του μοντέλου, τη διαδικασία προσομοίωσης και τέλος την εξαγωγή των αποτελεσμάτων.  Πιο συγκεκριμένα, στο κεφάλαιο 2 παρουσιάζονται όλα τα απαραίτητα δεδομένα που λαμβάνει υπόψη του ο αλγόριθμος. Αυτά είναι η αρχική δομή του υλικού (π.χ. εδροκεντρωμένο, χωροκεντρωμένο, εξαγωνικό), η ατομική τους απόσταση μέσα στη μοναδιαία κυψελίδα, το κρυσταλλογραφικό επίπεδο που δρα η δύναμη, οι κρυσταλλογραφικές ατέλειες, οι συνοριακές συνθήκες, το στατιστικό σύνολο που ανήκει, η συνάρτηση δυναμικού που περιγράφει την αλληλεπίδραση των ατόμων του υλικού καθώς επίσης και τις αρχικές ταχύτητες και επιταχύνσεις σε όλα τα άτομα.

Στη συνέχεια στο κεφάλαιο 3, παρουσιάζεται η διαδικασία της προσομοίωσης έχοντας λάβει υπόψη τα παραπάνω δεδομένα. Αρχικά επιλέγεται ένας αλγόριθμος χρονικής ολοκλήρωσης. Οι τρείς πιο διαδεδομένοι αλγόριθμοι είναι: Verlet, Πρόβλεψης - Διόρθωσης (Predictor – Corrector), και Βατραχοδρασκελισμού (Leapfrog). Στη συνέχεια υπολογίζονται οι δυνάμεις μεταξύ των ατόμων ως η παράγωγος του δυναμικού, οι τάσεις, κινητική, δυναμική, ολική ενέργεια και τέλος η θερμοκρασία του συστήματος.

Στο κεφάλαιο 4, γίνεται μία αναφορά στην ισορροπία που πρέπει να επέλθει το σύστημά μας έπειτα από μία κάποια διέγερση. Κάθε φορά που το σύστημα μας αλλάζει κατάσταση, βρίσκεται εκτός ισορροπία για ένα μικρό χρονικό διάστημα. Από αυτό συνεπάγεται ότι το σύστημα δεν είναι ακίνητο (διακυμαίνεται γύρω από ένα σταθερό σημείο) αλλά καταλήγει σε μία νέα τιμή (διακυμαίνεται γύρω από μία νέα τιμή όπου σταδιακά αλλάζει με το χρόνο).

Στο κεφάλαιο 5 εισάγουμε κάποια αδιάστατα ή μειωμένα μεγέθη, που χρησιμοποιούνται στη μέθοδο της μοριακής δυναμικής ώστε να δουλεύουμε με τιμές κοντά στη μονάδα. Επίσης οι εξισώσεις κινήσεως γίνονται απλούστερες επειδή μερικοί αν όχι όλοι οι παράμετροι που ορίζονται στο μοντέλο είναι κοντά στη μονάδα. Κάνοντας αυτή τη διαδικασία δεν επηρεάζεται καθόλου η διαδικασία και το αποτέλεσμα και ο υπολογιστής χειρίζεται μικρότερους αριθμούς που σε αντίθετη περίπτωση (με πολλά ψηφία) μπορεί να δημιουργούνταν πρόβλημα υπέρβασης του ορίου ψηφιών (overflow-underflow) που μπορεί να πάρει μία μεταβλητή.

Τέλος στο κεφάλαιο 6 παρουσιάζονται 2 αριθμητικές εφαρμογές στις οποίες διερευνάμε τη μηχανική συμπεριφορά δοκιμίων σε θλίψη. Στη πρώτη εφαρμογή εξετάζουμε την συμπεριφορά του πυρήνα μολύβδου ενός ελαστομεταλλικού εφέρδανου (LRB) υπό θλιπτικό φορτίο και συγκεκριμένη θερμοκρασία. Παρατηρούμαι ότι το όριο και η παραμόρφωση διαρροής εξαρτώνται από τη ταχύτητα φόρτισης καθώς επίσης, από το προσανατολισμό της κρυσταλλικής δομής και τη θερμοκρασία κατά την οποία γίνεται η προσομοίωση.

Η ταχύτητα των άκαμπτων τοίχων είναι αρκετά μεγάλη πράγμα που οδηγεί σε αύξηση του ορίου διαρροής του υλικού. Ο προσανατολισμός της κρυσταλλικής δομής επιδρά στην αντοχή του δοκιμίου και συγκεκριμένα για το (111) τείνει να την αυξήσει.  Η δύναμη δρα στο επίπεδο (111) που αποτελεί σύστημα ολίσθησης για το εδροκεντρωμένο κυβικό (FCC). Δηλαδή οι γραμμοταξίες (dislocations) κινούνται με μεγαλύτερη ευκολία σε αυτό το επίπεδο και παρατηρείται ότι η πλαστική παραμόρφωση συμβαίνει με ολίσθηση σε γωνία .

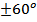Στη δεύτερη εφαρμογή εξετάζουμε την επίδραση του μεγέθους του δοκιμίου στη πλαστική περιοχή (size effects in plasticity)  ενός κρυσταλλικού υλικού δύο διαστάσεων υπό θλιπτικό φορτίο. Οι κρύσταλλοι μπορούν να γίνουν καλύτεροι (εμφανίζοντας π.χ. κράτυνση, strain-hardening), με μεγαλύτερη αντοχή, εισάγοντας τους κάποιες ατέλειες. Καθώς ο αριθμός των ατελειών αυξάνεται, η κίνηση τους παρεμποδίζεται επομένως ενισχύεται το υλικό, δηλαδή παρατηρείται μία σκλήρυνση (hardening).

Σύμφωνα με τις κλασσικές θεωρίες ελαστικότητας και πλαστικότητας, η θλίψη ενός δοκιμίου από συγκεκριμένο υλικό με συγκεκριμένη ονομαστική αντοχή είναι ανεξάρτητη από το μέγεθος της δομής του. Στη πραγματικότητα όμως, εξαιτίας της επίδρασης του μεγέθους του, το μεγαλύτερο δοκίμιο θα διαρρεύσει σε μικρότερη τάση απ’ ότι το μικρότερο.

Πειράματα σε μονοκρυσταλλικά υλικά (Fleck 1994, Ma και Clarke 1995, Nix και Gao 1998, Stolken και Evans 1998) έχουν δείξει ότι το όριο διαρροής  μειώνεται καθώς αυξάνεται ο αριθμός των ατόμων για δοκίμια μέχρι κάποια μικρόμετρα,  κρατώντας πάντα τις αναλογίες του δοκιμίου x και y σταθερές.

Για να διαπιστώσουμε την επίδραση του μεγέθους του δοκιμίου στη πλαστική περιοχή  εξετάζουμε 3 διαφορετικά δοκίμια διαφορετικού μεγέθους αλλά με ίδιες αναλογίες πλευρών. Κατασκευάζονται οι καμπύλες τάσεων – παραμορφώσεων για 3 διαφορετικά δοκίμια και κατόπιν παρουσιάζεται η επίδραση του μεγέθους του δοκιμίου με τη τάση διαρροής. Τέλος τα αποτελέσματα ελέγχονται με το μοντέλο των Ν. Scott Weingarten και R.L.B. Selinger 2011, που είχαν χρησιμοποιήσει παρόμοια δεδομένα προσομοίωσης αλλά είχαν κάνει χρήση της μεθόδου Monte Carlo.

Η συσχέτιση των δύο μεθόδων είναι αρκετά καλή και αποδεικνύεται ότι υπάρχει επίδραση του μεγέθους του δοκιμίου στο όριο διαρροής καθώς επίσης και στη μορφή της καμπύλης τάσεων παραμορφώσεων στη πλαστική περιοχή και με τη μέθοδο της μοριακής δυναμικής.