Στην Επιστήμη της Θραυστομηχανικής έχουν αναπτυχθεί διάφορα αριθμητικά μοντέλα τα οποία μπορούν να χωριστούν σε μοντέλα συνεχών συστημάτων (X-FEM, Mesh free method) και σε μοντέλα διακριτών συστημάτων (D.E.M., Lattice models). Το μοντέλο το οποίο αποτελεί το κύριο μέρος της εργασίας είναι το Σύστημα Στερεών Σωμάτων και ελατηρίων το οποίο επιλέχθηκε εξαιτίας της απλότητας του και της ικανότητάς του να προσομοιώσει το υλικό και τις ρωγμές στην κλίμακα του Μηχανικού.

 Η διαδικασία που ακολουθείται είναι η εξής. Αρχικά στο χωρίο διασκορπίζονται σημεία τα οποία αποτελούν και τους κόμβους του δικτύου. Για τα σημεία αυτά πρέπει οι αποστάσεις μεταξύ τους να είναι μεγαλύτερες από ένα όριο. Αυτό επιλέγεται για να υπάρχει ελαστική ομοιομορφία στο δίκτυο και να είναι αντικειμενικό  ως προς τη διάδοση της ρωγμής. Στη συνέχεια με βάση τα σημεία αυτά εφαρμόζεται η τεχνική Voronoi. Αυτή έχει ως αποτέλεσμα το χωρισμό του χωρίου σε κυρτά πολύγωνα τα οποία και αποτελούν τα στερεά σώματα του προσομοιώματος. Με βάση το διάγραμμα Voronoi τα πολύγωνα που δημιουργούνται χωρίζουν έτσι το χωρίο ώστε το σύνολο των σημείων που βρίσκονται εντός ενός πολυγώνου να είναι πιο κοντά στο κόμβο από τον οποίο προέκυψε το πολύγωνο παρά σε οποιονδήποτε άλλο κόμβο.

 

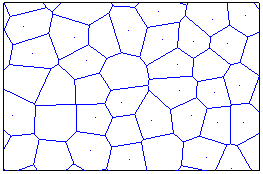
Εικόνα 1. Διάγραμμα Voronoi ορθογωνίου χωρίου.

 

Έχοντας μορφώσει τα στερεά σώματα από τα οποία θα αποτελείται το μοντέλο στη συνέχεια θεωρούμε ότι στο μέσο της κάθε διεπιφάνειας υπάρχουν 3 ελατήρια μηδενικού μήκους, ένα κάθετο στη διεπιφάνεια, ένα εφαπτομενικό και ένα στροφικό. Οι δυσκαμψίες τους είναι τέτοιες ώστε να προσομοιώνουν τις ελαστικές ιδιότητες του υλικού για δισδιάστατα προβλήματα.

Το στοιχείο του μοντέλου αποτελείται από 2 στερεά σώματα, τη διεπιφάνειά τους και τα 3 ελατήρια. Το μητρώο [Β] συσχετίζει τις σχετικές μετατοπίσεις των 3 ελατηρίων της διεπιφάνειας με τις μετατοπίσεις των κόμβων και αντίστροφα. Αν θεωρήσουμε το διαγώνιο μητρώο με τις δυσκαμψίες των 3 ελατηρίων τότε με βάση την αρχή των δυνατών έργων προκύπτει το μητρώο δυσκαμψίας του στοιχείου Κe=[Β]’[D][Β]. Από τα μητρώα δυσκαμψίας των μελών προκύπτει το μητρώο δυσκαμψίας της κατασκευής ακολουθώντας τη μέθοδο άμεσης ακαμψίας.

Αρχικά μελετήθηκε το απλό ελαστικό μοντέλο για στατική φόρτιση. Με γνωστό το μητρώο δυσκαμψίας της κατασκευής και το διάνυσμα των επικόμβιων δυνάμεων προκύπτουν οι μετατοπίσεις των κόμβων του φορέα με βάση τη γνωστή σχέση [Κ]{u}={f}.

 

Εικόνα 2. Αρχική και τελική κατάσταση αμφιέρειστης δοκού.

 

Στη συνέχεια αναπτύσσεται η θεωρία για την επίλυση του στατικού προβλήματος με τη δημιουργία ρωγμών. Η θραύση προκύπτει με απλό και εποπτικό τρόπο ελέγχοντας τις τάσεις σε κάθε υπολογιστικό βήμα σε κάθε διεπιφάνεια και μηδενίζοντας τις δυστένειες των ελατηρίων της διεπιφάνειας που ικανοποιούν το κριτήριο θραύσης. Στην παρούσα εργασία ως κριτήριο θραύσης επιλέχθηκε ένα απλό κριτήριο τύπου Mohr-Coulomb για τις ορθές και διατμητικές τάσεις. Παρουσιάζονται παραδείγματα που αναδεικνύουν την ικανότητα του μοντέλου να προσομοιώσει ρωγμές σε διάφορους απλούς φορείς.

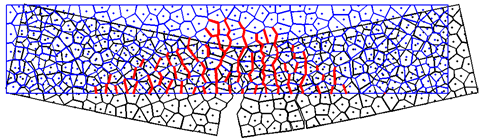
Εικόνα 3. Αρχική και τελική κατάσταση αμφιέρειστης δοκού με ρωγμές.

 

Περνώντας στο δυναμικό πρόβλημα απαιτείται η μόρφωση του μητρώου μάζας της κατασκευής. Αυτό προκύπτει για κάθε κόμβο από τη μάζα κάθε στερεού σώματος. Το μητρώο απόσβεσης που προκύπτει στη συνέχεια είναι τύπου Reyleigh και προκύπτει από το μητρώο μάζας και το μητρώο δυσκαμψίας της κατασκευής. Για την επίλυση της διαφορικής εξίσωσης κίνησης του φορέα το σύστημα των εξισώσεων μετατρέπεται σε μορφή χώρου κατάστασης. Για τα παραπάνω παρουσιάζονται παραδείγματα για δυναμική φόρτιση.

 

Εικόνα 4. Σύγκριση αποτελεσμάτων RBSN (64 και 275 σημεία) με ένα στοιχείο δοκού για ημιτονοειδή δυναμική φόρτιση.

 

Τέλος στο μοντέλο των Στερεών Σωμάτων και Ελατηρίων εφαρμόσθηκε το προσομοίωμα του Bouc-Wen. Αυτό είναι ένα υστερητικό προσομοίωμα και χρησιμοποιείται στην ελαστοπλαστική ανάλυση. Στις διεπιφάνειες τα ελατήρια θεωρήθηκε πλέον ότι συμπεριφέρονται ελαστοπλαστικά και ότι οι μετατοπίσεις χωρίζονται σε ένα ελαστικό και ένα υστερητικό μέρος. Το υστερητικό μέρος των μετατοπίσεων ακολουθεί τη διαφορική εξίσωση του Bouc-Wen. Η μέθοδος παρουσιάζεται θεωρητικά και ακολουθούν και παραδείγματα σε απλούς φορείς που επιβεβαιώνουν την εφαρμογή της.

 

Εικόνα 5. Διάγραμμα Δύναμης – Παραμόρφωσης για τα εσωτερικά ελατήρια με βάση το προσομοίωμα Bouc-Wen.