Σχήμα I:            Παράδειγμα προσδιορισμού της χρονικής στιγμής t_L,gr.

Στη συνέχεια, εφαρμόζεται η μεθοδολογία για το δεδομένο αυτό t_L,gr έτσι ώστε να ελεγχθεί εάν πράγματι οδηγεί σε ικανοποιητική πρόβλεψη της εδαφικής συμπεριφοράς.

Οι αναλύσεις που αντιστοιχούν στο πρώτο τμήμα της δόνησης (t ≤ t_L,gr) πραγματοποιούνται θεωρώντας πλήρη απουσία ρευστοποίησης, δηλαδή θεωρώντας μηδενικό συντελεστή υπερπιέσεων πόρων (r_u = 0). Για τις αναλύσεις που αντιστοιχούν στο δεύτερο τμήμα της δόνησης (t > t_L,gr), υιοθετείται η μεθοδολογία των Miwa & Ikeda (2006), καθώς το ελαστικό μέτρο διάτμησης G_max μειώνεται σε μια συγκεκριμένη σταθερή τιμή (G_liq = ρV_S,liq²), ενώ η τιμή του λόγου υστερητικής απόσβεσης ξ είναι συνάρτηση της επιβαλλόμενης διατμητικής παραμόρφωσης γ, όπως αυτή προκύπτει από τις τυπικές καμπύλες ξ-γ για άμμους. Οι εν λόγω αναλύσεις πραγματοποιούνται στην παρούσα φάση για τη βέλτιστη ταχύτητα μετάδοσης σεισμικού κύματος στο ρευστοποιημένο έδαφος V_S,liq, η οποία προκύπτει παραμετρικά. Πιο συγκεκριμένα, γίνονται ισοδύναμες γραμμικές αναλύσεις για ολόκληρη τη δόνηση χρησιμοποιώντας διαφορετικές τιμές του λόγου της ταχύτητας V_S,liq με την αντίστοιχη ταχύτητα V_S,o των σεισμικών κυμάτων πριν την ρευστοποίηση (V_S,liq/V_S,o) και επιλέγεται η καταλληλότερη τιμή που επιτυγχάνει τη βέλτιστη πρόβλεψη του πραγματικού φάσματος σε μεγάλες περιόδους.

Η σύγκριση μεταξύ των αριθμητικών αναλύσεων (FLAC) και των απλοποιημένων αναλύσεων με την προτεινόμενη μεθοδολογία γίνεται συγκρίνοντας τις μέσες φασματικές τιμές σε τέσσερα εύρη περιόδων (Τ = 0-0.15sec, 0.15-0.40sec, 0.40-0.80sec και 0.80-1.60sec). Διαπιστώνεται μία υπερεκτίμηση των τιμών στις μικρές περιόδους του φάσματος, εύρος που επηρεάζεται από το κομμάτι της δόνησης πριν τη ρευστοποίηση. Για το λόγο αυτό, επαναλήφθηκαν οι αναλύσεις για t ≤ t_L,gr θεωρώντας μειωμένη ταχύτητα διατμητικών κυμάτων καθ’ ύψος της στήλης του εδάφους, καθώς στο κομμάτι αυτό της δόνησης έχουν ήδη αναπτυχθεί σημαντικές υπερπιέσεις πόρων. Τελικά, επιλέγεται λόγος 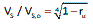 που αντιστοιχεί σε λόγο υπερπίεσης πόρων   r_u = 0.6.

Η σύγκριση των τελικών φασμάτων (Σχήμα II) θεωρείται ικανοποιητική, καθώς μετά από στατιστική επεξεργασία των αποτελεσμάτων διαπιστώνεται ένα μέσο σφάλμα στην τελική εκτίμηση των φασματικών τιμών της τάξης του 13% για τις μικρές περιόδους (T = 0-0.80 sec) και 1% για τις μεγαλύτερες. Συνεπώς, συμπεραίνεται ότι η μέθοδος μπορεί να οδηγήσει σε επιτυχημένη πρόβλεψη της εδαφικής συμπεριφοράς με αποκλίσεις οι οποίες είναι υπέρ της ασφαλείας. Πηγή αβεβαιοτήτων για την πρακτική εφαρμογή της παραμένει η πρόβλεψη του t_L,gr και η ορθή εκτίμηση του λόγου V_S,liq/V_S,o.

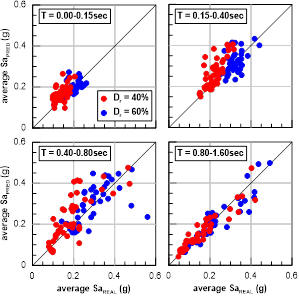
Σχήμα II:           Σύγκριση μέσων φασματικών επιταχύνσεων θεωρώντας r_u = 0.6 στο πρώτο τμήμα (t ≤ t_L,gr).

 

Πρόβλεψη της επιφανειακής εκδήλωσης ρευστοποίησης t_L,gr

Στις αριθμητικές αναλύσεις, η χρονική στιγμή έναρξης της ρευστοποίησης t_L σε κάθε βάθος μπορεί να προσδιοριστεί με ακρίβεια μέσω των αντίστοιχων χρονοϊστοριών του r_u. Σε πρακτικές εφαρμογές, με δεδομένο μόνο την κατανομή του FS_L με το βάθος, η οποία έχει εκτιμηθεί σύμφωνα με την εμπειρική μεθοδολογία Youd et al. (2001), ο χρόνος έναρξης της ρευστοποίησης μπορεί να εκτιμηθεί ως εξής:

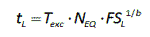
όπου b η κλίση της καμπύλης ρευστοποίησης της άμμου και T_exc, N_EQ η θεμελιώδης περίοδος και οι ισοδύναμοί κύκλοι της διέγερσης αντίστοιχα. Τυπικά εύρη τιμών για την κλίση b είναι b = 0.3 ÷ 0.4. Για τη χρήση της προηγούμενης εξίσωσης απαιτείται η προσεγγιστική μετατροπή της ανομοιόμορφης δόνησης σχεδιασμού σε ισοδύναμη ομοιόμορφη με Ν_EQ κύκλους φόρτισης, περίοδο Τ_exc και σταθερό εύρος επιτάχνυνσης, ίσο με την «ενεργό» επιτάχυνση a_eff ως εξής:

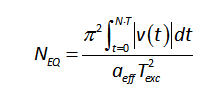
όπου v(t) είναι η χρονοϊστορία της ταχύτητας της διέγερσης. Επισημαίνεται ότι η σχέση αυτή ισχύει με απόλυτη ακρίβεια για αρμονικές διεγέρσεις, ενώ έχει επιβεβαιωθεί η αξιοπιστία της στην αναλυτική πρόβλεψη φαινομένων ρευστοποίησης υπό πραγματικές διεγέρσεις (Karamitros et al. 2013). Ως θεμελιώδης περίοδος της διέγερσης T_exc λαμβάνεται η μέση περίοδος του τμήματος του φάσματος επιταχύνσεων για το οποίο ισχύει Sa > 2.5PGA (PGA: μέγιστη εδαφική επιτάχυνση), ενώ η «ενεργός» επιτάχυνση a_eff υπολογίζεται ως εξής (Tokimatsu & Yoshimi 1983):

Εν συνεχεία, προσδιορίζεται κάθε φορά η μέση και η ελάχιστη τιμή του χρόνου ρευστοποίησης οι οποίες συγκρίνονται με το γνωστό t_L,gr. Ικανοποιητική γραμμική συσχέτιση παρουσιάζεται για την ελάχιστη τιμή του t_L καθ’ ύψος της στήλης t_L,min και συγκεκριμένα: t_L,gr = 0.84∙t_L,min . Επιπρόσθετα, για να επιτευχθούν προβλέψεις υπέρ της ασφαλείας, προτείνεται και ένα άνω όριο: t_L,gr = 0.95∙t_L,min. (Σχήμα III).

Σχήμα III:          Σύγκριση t_L,gr - ελάχιστης τιμής του t_L για το σύνολο των αναλύσεων και προτεινόμενα κριτήρια πρόβλεψης.

 

Αξιολόγηση μεθοδολογίας - Εφαρμογή για προβλεπόμενο t_L,gr

Στο τελευταίο κεφάλαιο της Μεταπτυχιακής Εργασίας παρουσιάζονται τα βήματα της μεθοδολογίας πρόβλεψης ελαστικών φασμάτων απόκρισης σε ρευστοποιήσιμο έδαφος «με επαλληλία» με όλες τις προτεινόμενες τροποποιήσεις της βαθμονόμησης της και κατόπιν εφαρμόζεται βήμα προς βήμα για τις εξεταζόμενες περιπτώσεις. Τα βασικά σημεία στα οποία θα πρέπει να εστιάσει ο μελλοντικός χρήστης είναι τα ακόλουθα:

·         Για t ≤ t_L,gr πρέπει να ληφθεί μειωμένη ταχύτητα διατμητικών κυμάτων η οποία να αντιστοιχεί σε λόγο υπερπίεσης πόρων r_u = 0.4 – 0.6.

·         Για t > t_L,gr μπορεί να λαμβάνεται ο λόγος V_S,liq/V_S,o συναρτήσει του μέσου καθ’ ύψος FS_L, σύμφωνα με τα προτεινόμενα εύρη των Miwa & Ikeda (2006) τα οποία φαίνονται στον ακόλουθο Πίνακα I. Πρέπει να σημειωθεί ότι οι μέσες τιμές του Πίνακα Ι είναι συστηματικά μεγαλύτερες από τους βέλτιστους λόγους που προέκυψαν από την παραμετρική διερεύνηση, με αποτέλεσμα το σχετικό σφάλμα στις μεγάλες περιόδους να αυξάνεται σημαντικά -περί το 20%- πάντα όμως υπέρ της ασφαλείας. Προτείνεται, λοιπόν, η χρήση των κατώτατων ορίων, ειδικά για μικρές σχετικές πυκνότητες (π.χ.          D_r ≤ 40%).

I:        Προτεινόμενες τιμές του λόγου V_S,liq/V_S,o κατά Miwa & Ikeda (2006).

 ·         Η πρόβλεψη της χρονικής στιγμής επιφανειακής εκδήλωσης της ρευστοποίησης μπορεί να γίνει σύμφωνα με τη σχέση:

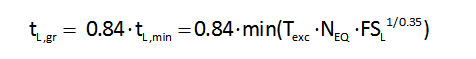
Η χρήση της προτεινόμενης σχέσης οδηγεί σε σχετικό σφάλμα της τάξης του 13% για Τ < 0.40sec και 20% περίπου για περιόδους μεταξύ Τ = 0.40 - 1.60sec. Τα αποτελέσματα της σύγκρισης των μέσων φασματικών επιταχύνσεων παρουσιάζονται στο Σχήμα IV.

IV:          Σύγκριση μέσων φασματικών επιταχύνσεων θεωρώντας την μέση εκτίμηση του t_L,gr.

·         Συντηρητική εκτίμηση του ελαστικού φάσματος μπορεί να επιτευχθεί με το άνω όριο του t_L,gr (ήτοι    t_L,gr = 0.95∙t_L,min) και το κάτω όριο του r_u για το πρώτο τμήμα της δόνησης (ήτοι r_u = 0.4). Η υπερεκτίμηση που παρέχει είναι της τάξης του 34% για τις μικρές περιόδους (T = 0 - 0.80 sec) και 20% για τις μεγαλύτερες.