Η ανάλυση των κατασκευών και ο ασφαλής, λειτουργικός και οικονομικός σχεδιασμός τους αποτελούν αντικείμενο εργασίας και στόχο ενός πολιτικού μηχανικού. Η ασφάλεια επιτάσσει η κατασκευή να διατηρεί την στατική της επάρκεια ακόμη και υπό τις δυσμενέστερες φορτίσεις που μπορεί να τις επιβληθούν στον χρόνο ζωής της, ενώ η λειτουργικότητα να εκπληρώνει απρόσκοπτα την λειτουργία για την οποία σχεδιάστηκε στις συνήθεις συνθήκες. Από την άλλη πλευρά η οικονομία αποτρέπει τον μελετητή από την επιλογή υπερδιαστασιολόγησης και οδηγεί σε επιλογές που εκμεταλλεύονται στον μέγιστο βαθμό τα περιθώρια αντοχών της.

Η ταυτόχρονη ικανοποίηση ασφαλούς σχεδιασμού και πλήρους εκμετάλλευσης των διαθέσιμων αντοχών εντοπίζεται ακριβώς την στιγμή πριν την αστοχία της κατασκευής, όπου ο όρος αστοχία μπορεί να αναφέρεται στην μετατροπή της κατασκευής σε μηχανισμό (κατάρρευση), στην υπέρβαση προκαθορισμένων επιτρεπόμενων παραμορφώσεων ή σε όποια άλλη κατάσταση ο μηχανικός θέτει ως οριακή στον σχεδιασμό του.

Στην περίπτωση που η αστοχία ταυτίζεται με την κατάρρευση έχει αναπτυχθεί πληθώρα μεθόδων ανάλυσης της κατασκευής. Σε κάθε πρόβλημα μπορεί να επιδιώκεται διαφορετικό ζητούμενο, όπως για παράδειγμα η μεγιστοποίηση των φορτίων για δεδομένο σχεδιασμό ή η ελαχιστοποίηση του βάρους για δεδομένη φορτιστική κατάσταση. Οι περισσότερες μέθοδοι παρακολουθούν την ελαστική και ανελαστική συμπεριφορά της έως την κατάρρευση. Όμως το οριακό φορτίο (φορτιστικός συντελεστής κατάρρευσης α) ή το ελάχιστο βάρος w και η οριακή μορφή είναι δυνατόν να υπολογιστούν και απευθείας με εφαρμογή μεθόδων οριακής ανάλυσης.

Η οριακή ανάλυση βασίζεται στην παραδοχή τελείως πλαστικής συμπεριφοράς υλικού. Η μαθηματική διατύπωση του προβλήματος με χρήση μητρωικού λογισμού σε συνδυασμό με τα βασικά θεωρήματα της οριακής ανάλυσης (στατικό, κινηματικό και θεώρημα μοναδικότητας λύσης) επιτρέπουν την επίλυσή του με εφαρμογή μεθόδων μαθηματικού προγραμματισμού. Ο μαθηματικός προγραμματισμός οδηγεί στον υπολογισμό βέλτιστης λύσης που ικανοποιεί προκαθορισμένους περιορισμούς και τοιουτοτρόπως μπορεί να προσδιοριστεί η τελική κατάσταση μιας κατασκευής στην οποία να ικανοποιούνται οι συνθήκες ισορροπίας και συμβιβαστού.

Στην περίπτωση που το υλικό είναι στερεό-ιδεωδώς πλαστικό, τα κριτήρια διαρροής διατομής είναι γραμμικοποιημένα, και δεν υπάρχουν περιορισμοί στις παραμορφώσεις της κατασκευής, το πρόβλημα που μορφώνεται εντάσσεται στην κατηγορία προβλημάτων βελτιστοποίησης γραμμικού προγραμματισμού.

Γενικά και σύμφωνα με τον [Rao (2009)] το πρόβλημα γραμμικού προγραμματισμού μπορεί να διατυπωθεί ως

ενώ συγκεκριμένα το στατικό θεώρημα της οριακής ανάλυσης μπορεί να διατυπωθεί ως πρόβλημα γραμμικού προγραμματισμού με την μορφή:

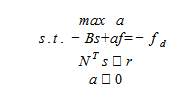
όπου 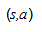 οι μεταβλητές σχεδιασμού, με α τον φορτιστικό συντελεστή.

Για την επίλυση προβλημάτων LPs υπάρχουν πολλοί, διαφορετικοί αλγόριθμοι. Καθένας εξ αυτών εμφανίζει πλεονεκτήματα ή μειονεκτήματα που τον καθιστούν κατάλληλο ή μη κατάλληλο για τα είδη προβλημάτων που καλείται να λύσει. Κατηγοριοποιούνται με βάση διάφορα χαρακτηριστικά τους και ένα βασικό στοιχείο διαχωρισμού αποτελεί το αν είναι εσωτερικού σημείου ή συνόρου - simplex.

Οι δύο αλγόριθμοι που επελέγησαν στο πλαίσιο της παρούσας εργασίας κατατάσσονται στους αλγορίθμους εσωτερικού σημείου και επίσης ανήκουν στους γεωμετρικούς αλγόριθμους. Ο πρώτος ονομάζεται ελλειψοειδής (Ellipsoid Method), αναπτύχθηκε από τον Kachiyan το 1979 και πρόκειται για τον πρώτο αλγόριθμο που αποδεικνύει ότι το πρόβλημα γραμμικού προγραμματισμού επιλύεται σε πολυωνυμικό χρόνο. Παρότι από θεωρητικής πλευράς ο αλγόριθμος ελλειψοειδούς είναι μαθηματικά άρτιος και πολύ σημαντικός ιστορικά, σε πρακτικό επίπεδο και συγκρινόμενος με άλλες μεθόδους λειτουργεί πολύ αργά και χρειάζεται μεγάλο αριθμό επαναλήψεων για να συγκλίνει.

Αρχικό στόχο της εργασίας αποτέλεσε η βελτίωση του αλγορίθμου, ώστε να λειτουργεί γρηγορότερα, καθώς και η εφαρμογή του σε προβλήματα οριακής ανάλυσης. Τόσο η εκτεταμένη βιβλιογραφική έρευνα όσο και πειραματικές αναλύσεις με χρήση Matlab έδειξαν ότι μικρές αλλαγές που μπορούν να εφαρμοστούν στον αλγόριθμο δεν αποδεικνύονται ικανές να τον βελτιώσουν τόσο, ώστε να γίνει ανταγωνιστικός ως προς άλλους χρησιμοποιούμενους αλγορίθμους, όπως την μέθοδο Simplex ([Dantzig 1947]) ή την IPM του Karmakar. Ειδικά για την περίπτωση προβλημάτων οριακής ανάλυσης, η εκμετάλλευση των οριακών τιμών στις μεταβλητές σχεδιασμού s, που ταυτίζονται με τις αντοχές των διατομών, επέτρεψε την χρήση του αλγορίθμου σε προβλήματα μεγάλου μεγέθους, χωρίς όμως να βελτιώνεται η απόδοσή του. Βεβαίως, στην περίπτωση που αγνοήθηκαν τα όρια αυτά ο αλγόριθμος τερμάτιζε πολύ νωρίς επειδή η τιμή της ακτίνας του αρχικού κύκλου ήταν άπειρη (inf).

Λόγω της μεγάλης θεωρητικής αξίας του αλγορίθμου, τμήμα της εργασίας αφιερώθηκε στην συγκέντρωση και ανάλυση των μαθηματικών αποδείξεων των επιμέρους θεωρημάτων, λημμάτων και προτάσεων που τελικά οδηγούν στην άρτια θεμελίωσή του. Επίσης, κάνοντας χρήση του κώδικα Matlab της μεθόδου ελλειψοειδούς που δημιουργήθηκε στο πλαίσιο μεταπτυχιακής εργασίας του F. Stallmann (2014) και διατίθεται στο διαδίκτυο επιλύθηκαν παραδείγματα οριακής ανάλυσης. Η απόδοση της μεθόδου σε σχέση με την linprog που διαθέτει εγγενώς η Matlab είναι όντως αποκαρδιωτική. Ενδεικτικά αναφέρεται ότι στις 6 επαναλήψεις της linprog αντιστοιχούσαν περί τις 6500 επαναλήψεις της μεθόδου ελλειψοειδούς, στις 15 της linprog περίπου 50000 της ελλειψοειδούς, ενώ όσο το μέγεθος του στιγμιοτύπου μεγάλωνε, τόσο η διαφορά γινόταν μεγαλύτερη.

Ο δεύτερος αλγόριθμος που μελετήθηκε είναι ο αλγόριθμος ή μέθοδος σφαίρας (Sphere method), ο οποίος μετά την αρχική του διατύπωση το 2005 ([Murty 2005]), βελτιώθηκε και δημοσιεύτηκαν 5 παραλλαγές του έως και σήμερα. Ο συγκεκριμένος αλγόριθμος κατατάσσεται στους αλγορίθμους διόρθωσης και πρόβλεψης. Κάθε γενική επανάληψή του αποτελείται από δύο διακριτά υπολογιστικά σκέλη: το κεντροποιόν βήμα, με το οποίο διορθώνεται η λύση στην οποία είχε καταλήξει η προηγούμενη επανάληψη, και το βήμα καθόδου, με το οποίο γίνεται υπολογισμός της επόμενης λύσης.

Ως μέθοδος μοιράζεται κοινά στοιχεία με τον προπομπό της, την μέθοδο βαρύτητας (Gravitational Method, [Chang, Murty (1989)]), δεδομένου ότι στο βήμα καθόδου ακολουθεί την λογική της “πτώσης” ενός σημείου στο οποίο επιδρά βαρυτικό πεδίο. Ωστόσο λόγω του κεντροποιού βήματος οι δύο μέθοδοι διαφοροποιούνται σημαντικά. Η μέθοδος βαρύτητας ανήκει στις μεθόδους συνόρου, ενώ η σφαίρας στις μεθόδους εσωτερικού σημείου.

 Οι ερευνητές που ανέπτυξαν την οικογένεια των μεθόδων σφαίρας (Murty, Oskoorouchi, Kabadi), διατείνονται ότι αυτές λειτουργούν ταχύτερα από τους υπάρχοντες αλγόριθμους σε διάφορους τύπους προβλημάτων γραμμικού προγραμματισμού. Η διαφορά γίνεται πιο έντονη όσο μεγαλώνει το μέγεθος του στιγμιοτύπου, αυξάνει η πυκνότητα (density) του μητρώου συντελεστών και οι περιορισμοί γίνονται σημαντικά περισσότεροι από τις μεταβλητές, m>>n. Στο πρόβλημα οριακής ανάλυσης με χρήση στατικού θεωρήματος ισχύει m>>n και τα στιγμιότυπα μεγαλώνουν πολύ σε μέγεθος όταν πρόκειται για πραγματικές κατασκευές. Τα μητρώα των συντελεστών, βεβαίως, δεν είναι πολύ πυκνά, ούτε όμως και τελείως sparse. Για παράδειγμα, στις περιπτώσεις που εξετάστηκαν εδώ τα μητρώα εμφάνιζαν μια πυκνότητα από ~ 5 % έως ~ 23 %.

 Τα παραπάνω εγείρουν το ενδιαφέρον, διότι υπάρχει η πιθανότητα η εφαρμογή των αλγορίθμων σφαίρας σε προβλήματα οριακής ανάλυσης να μειώνει σημαντικά τους χρόνους επίλυσής αυτών με υπολογιστή. Για τον λόγο αυτό αποφασίστηκε στην παρούσα εργασία τα παραδείγματα που λύθηκαν με την μέθοδο ελλειψοειδούς να λυθούν και με κάποια μέθοδο σφαίρας. Για την τελευταία ήταν αναγκαίο να γραφεί κώδικας στην Matlab. Επελέγη η SM1 (Sphere method 1), η οποία αποτελεί την βάση και για τις άλλες SMs, δεδομένου ότι εκείνες προκύπτουν μέσω βελτιώσεων της πρώτης, και μπορεί έτσι να χρησιμοποιηθεί ως οδηγός για μελλοντικό προγραμματισμό και των υπολοίπων SMs. Ο κώδικας γράφτηκε ακολουθώντας ακριβώς όσα αναφέρονται στην βιβλιογραφία για την SM1 ([Murty 2006a], [Murty 2006b]).

Πριν την εφαρμογή του κώδικα της SM1 στα προβλήματα οριακής ανάλυσης, έγινε δοκιμή του σε πρόβλημα μητρώου 3x2 στο οποίο και λειτούργησε κανονικά. Το ίδιο συνέβη και σε ορισμένες περιπτώσεις των παραδειγμάτων οριακής ανάλυσης που εξετάστηκαν. Ωστόσο, παρατηρήθηκε ότι όσο το μέγεθος των στιγμιοτύπων μεγάλωνε, ο αλγόριθμος “εγκλωβιζόταν” σε σημεία και αδυνατούσε να δώσει λύση. Το σε ποια επανάληψη συνέβαινε αυτός ο “εγκλωβισμός” και ποια τιμή είχε υπολογίσει έως τότε επηρεαζόταν από τις παραμέτρους M, p της big-M augmentation διαδικασίας και τις ανοχές ε που χρησιμοποιούνταν. Παρά τα προβλήματα και την αδυναμία επίλυσης, το ποσοστό μείωσης της τιμής της αντικειμενικής συνάρτησης στα πρώτα βήματα που εκτελούνταν πάντοτε κανονικά ήταν πολύ μεγάλο (της τάξης του 90%).

 Κατά την γνώμη της συγγράφουσας της παρούσας εργασίας η παρατηρούμενη δυσλειτουργία μπορεί να οφείλεται καταρχάς στις χρησιμοποιούμενες στον κώδικα παραμέτρους και ανοχές. Για να βρεθούν οι τιμές  εκείνες που σταθεροποιούν τον αλγόριθμο απαιτείται η επίλυση αρκετών στιγμιοτύπων, ώστε να μπορεί γίνει αντιληπτός ο ακριβής τρόπος με τον οποίο επηρεάζουν την λειτουργία του και να επιλεγούν τελικά οι βέλτιστες για κάθε μέγεθος στιγμιοτύπου. Επίσης, δεύτερος λόγος που οδηγεί σε παρέκκλιση της λειτουργίας από την επιθυμητή μπορεί να είναι ότι τα προβλήματα οριακής ανάλυσης περιέχουν εξ αρχής μεγάλο πλήθος ισοτικών περιορισμών, οι οποίοι χρειάζεται να μετατραπούν σε διπλές ανισότητες και στην συνέχεια να εφαρμοστεί η big-M augmentation διαδικασία, ώστε το χωρίο λύσεων να αποκτήσει μη κενό εσωτερικό. Με αυτόν τον τρόπο όμως ο χώρος όπου μπορεί να κινηθεί το εσωτερικό σημείο στην SM1 γίνεται από κάποια επανάληψη και μετά πολύ μικρού όγκου, γεγονός που δυσχεραίνει την εκτέλεσή του, αρκετά πριν γίνει μια ικανοποιητική προσέγγιση της λύσης.

Εντούτοις και παρά τα ζητήματα που προαναφέρθηκαν, η μέθοδος σφαίρας φαίνεται πολλά υποσχόμενη. Κρίνεται ενδιαφέρον να προγραμματιστούν και οι υπόλοιπες εκδοχές της και να ερευνηθούν και να συγκριθούν η λειτουργία, η αποτελεσματικότητα και η απόδοσή τους σε διάφορες μορφές και μεγέθη στιγμιοτύπων. Επιπρόσθετα, και αφού ελεγχθούν με χρήση γλώσσας προγραμματισμού Matlab ή άλλης παρεμφερούς, κρίνεται χρήσιμο να προγραμματιστούν και σε lower ή low-level γλώσσες προγραμματισμού, ώστε εκτός του αριθμού των επαναλήψεων να καταστούν συγκρίσιμοι και οι χρόνοι επίλυσης των διαφόρων στιγμιοτύπων με προϋπάρχοντες αλγορίθμους. Αν οι αλγόριθμοι γίνουν ευσταθείς και λειτουργήσουν όπως προοιωνίζεται από τις πρώτες δοκιμές, θα επιταχύνουν σημαντικά την επίλυση προβλημάτων οριακής ανάλυσης.