Η ανάλυση αξιοπιστίας είναι ένα
επιστημονικό πεδίο, που σκοπό έχει να αντιμετωπίσει
προβλήματα με αβεβαιότητες, με τρόπο πιθανοτικό. Στην
αξιοπιστία των κατασκευών τέτοιες αβεβαιότητες είναι
συνήθεις, και πηγάζουν από τις ιδιότητες των υλικών, τη
γεωμετρία του φορέα, την κατασκευή, τη μαθηματική
προσομοίωση, τα επιβαλλόμενα φορτία. Η πιο κοινή
αντιμετώπιση τέτοιων προβλημάτων είναι ο διαχωρισμός των
αβέβαιων μεγεθών σε ευμενή και δυσμενή, και η χρήση
μειωτικών και αυξητικών συντελεστών αντίστοιχα. Αυτή η
προσέγγιση, ωστόσο, είναι αδύνατη σε μη-γραμμικά
προβλήματα, όπου η αρχή της επαλληλίας δεν ισχύει, και
ενδεχομένως οδηγεί σε υπερσυντηρητικό σχεδιασμό. Από την
άλλη, η πιθανοτική αντιμετώπιση, απαιτεί μονάχα τον
προσδιορισμών των αβεβαιοτήτων, με συναρτήσεις
συχνότητας πιθανότητας (ΣΣΠ), προκειμένου να παρέχει την
μέτρηση ενός πιθανού σεναρίου, όπως αυτά της αστοχίας
και της ασφάλειας, και εν τέλει της δομικής αξιοπιστίας.
Η επίλυση ενός προβλήματος
αξιοπιστίας, επιτυγχάνεται με διάφορους τρόπους. Από
αυτούς, οι αναλυτικοί τρόποι είναι ευθείς, όμως
εξαιρετικά περιορισμένοι και ανεφάρμοστοι σε πολύπλοκα
προβλήματα. Άλλες μέθοδοι, όπως αυτές που βασίζονται στη
γνώση της παραγώγου, είναι αποτελεσματικές υπό
προϋποθέσεις, και μπορούν να αντιμετωπίσουν
προσεγγιστικά, μόνο κάποια είδη προβλημάτων. Οι
επικρατέστερες μέθοδοι, είναι αριθμητικές, και
προσομοιώνουν πειράματα τύχης σε υπολογιστή. Η πιο
γνωστή και εύρωστη μέθοδος είναι η προσομοίωση Monte
Carlo (MCS), που παρέχει πολυπληθή αποτελέσματα από
προσομοιώσεις, τα οποία ταξινομούνται στο αντίστοιχο
πεδίο (π.χ. της ασφάλειας ή της αστοχίας), ώστε να
ληφθεί συμπέρασμα για τη συχνότητα εμφάνισης ενός
φαινομένου. Η προσομοίωση Monte Carlo και οι παραλλαγές
της, όπως η προσομοίωση με τη μέθοδο των υποσυνόλων
(Subset Simulation ή SS), είναι οι πιο προτιμητέες για
την αντιμετώπιση προβλημάτων αξιοπιστίας.
Η εργασία αυτή παρουσιάζει ένα
τρόπο αντιμετώπισης του μεγαλύτερου μειονεκτήματος των
μεθόδων προσομοίωσης. Όπως προαναφέρθηκε, αυτές οι
μέθοδοι βασίζονται σε επαναληπτικές διαδικασίες. Συνεπώς
η συνάρτηση αστοχίας gx , που καθορίζει την ταξινόμηση
μίας πιθανής κατάστασης, υπολογίζεται διαδοχικά πολλές
φορές. Αυτό σημαίνει, ότι το υπολογιστικό κόστος είναι
υψηλό, και η διαδικασία χρονοβόρα, διότι η συνάρτηση
αστοχίας μπορεί να περιλαμβάνει πολύπλοκά μοντέλα
πεπερασμένων στοιχείων, ανάλυση χρονοϊστορίας κ.α.. Η
κύρια ιδέα για την αντιμετώπιση αυτής της δυσκολίας,
είναι η αντικατάσταση της συνάρτησης αστοχίας, με μία
νέα, που μπορεί να παρέχει αξιόπιστη ταξινόμηση και
εύκολα υπολογίσιμη. Αυτή η συνάρτηση ονομάζεται
αδρομερές μοντέλο και είναι βασιζόμενο σε πολύ
περιορισμένη γνώση της πραγματικής συνάρτησης αστοχίας.
Η εργασία, λοιπόν, επικεντρώνεται στη γραμμική πρόβλεψη
kriging ως αδρομερές μοντέλο στη δομική αξιοπιστία.
Στο πρώτο κεφάλαιο
παρουσιάζονται όλα τα βασικά θεωρητικά στοιχεία στα
οποία βασίζεται η ανάλυση αξιοπιστίας σε μοντέλο
kriging. Αρχικά ορίζονται οι τυχαίες μεταβλητές και
διανύσματα, καθώς οι βασικότερες κατανομές, όπως η
κανονική, η λογαριθμοκανονική και η ακροτάτων (Gumbel),
με βάση τις οποίες προσομοιώνονται οι αβεβαιότητες των
μεγεθών. Στη συνέχεια ορίζεται η στοχαστική ανέλιξη, που
αποτελεί τη βάση της πρόβλεψης kriging. Στα πλαίσια
αυτής της εργασίας οι στοχαστικές ανελίξεις
περιορίζονται στις Γκαουσιανές. Επιπλέον, γίνεται η
απλοποίηση, ότι το μητρώο συσχετίσεως, προκύπτει από
συναρτήσεις συσχέτισης, οι οποίες συναρτάνε τη συσχέτιση
με την απόσταση στο χώρο των εισαγόμενων μεταβλητών, και
ρυθμίζονται από τους συντελεστές συσχέτισης. Η πρόβλεψη
kriging, ή αλλιώς η βέλτιστη αμερόληπτη (unbiased)
γραμμική πρόβλεψη, στοχεύει στον προσδιορισμό μίας
στοχαστικής ανέλιξης, βασιζόμενη σε παρατηρήσεις, δηλαδή
ένα πεπερασμένο σύνολο σημείων του πεδίου ορισμού της
συνάρτησης αστοχίας, με τις αντίστοιχες τιμές της. Η
εύρεση των συντελεστών συσχέτισης γίνεται επιλύοντας ένα
υπολογιστικά δύσκολο πρόβλημα βελτιστοποίησης. Με αυτόν
τον τρόπο, η πρόβλεψη kriging παρέχει το μοντέλο
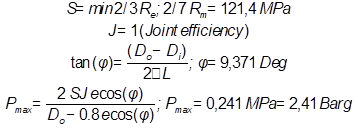 ,
δηλαδή για το τυχόν σημείου του πεδίου ορισμού, δίνεται
η μέση τιμή μG(x) και η τυπική απόκλιση σG(x),
που περιγράφουν την εκτίμηση της συνάρτησης αστοχίας,
μαζί με την αντίστοιχη αβεβαιότητα. Ιδιότητα αυτού του
μοντέλου είναι ότι στα υποστηρικτικά σημεία
(παρατηρήσεις), η μέση τιμή μG(x) ταυτίζεται
με την g(x), ενώ η τυπική απόκλιση σG(x) είναι
μηδενική. Συνεπώς το μοντέλο kriging παρέχει στις
περιοχές κοντά στα υποστηρικτικά σημεία πιο βέβαιη
πρόβλεψη απ’ ότι πιο μακριά.
,
δηλαδή για το τυχόν σημείου του πεδίου ορισμού, δίνεται
η μέση τιμή μG(x) και η τυπική απόκλιση σG(x),
που περιγράφουν την εκτίμηση της συνάρτησης αστοχίας,
μαζί με την αντίστοιχη αβεβαιότητα. Ιδιότητα αυτού του
μοντέλου είναι ότι στα υποστηρικτικά σημεία
(παρατηρήσεις), η μέση τιμή μG(x) ταυτίζεται
με την g(x), ενώ η τυπική απόκλιση σG(x) είναι
μηδενική. Συνεπώς το μοντέλο kriging παρέχει στις
περιοχές κοντά στα υποστηρικτικά σημεία πιο βέβαιη
πρόβλεψη απ’ ότι πιο μακριά.
Στα προβλήματα ανάλυσης
αξιοπιστίας, απαιτείται η σωστή ταξινόμηση κάθε σημείου
του πεδίου ορισμού. Συνεπώς, το μοντέλο kriging
θεωρείται επαρκές όχι όταν παρέχει με βεβαιότητα κάθε
τιμή της g(x) , αλλά όταν παρέχει σωστή ταξινόμηση. Για
τον υπολογισμό της πιθανότητας αστοχίας, στην αξιοπιστία
κατασκευών, ορίζεται η συνάρτηση πιθανοτικής ταξινόμησης
π(x) που εκφράζει την πιθανότητα μία κατάσταση ή αλλιώς
ένα σημείο του χώρου να βρίσκεται στην περιοχή της
αστοχίας. Λαμβάνει τιμές από το μηδέν έως το ένα και
υπολογίζεται από τις προαναφερθέντες ποσότητες μG(x),σG(x).
Στο δεύτερο κεφάλαιο
παρουσιάζονται αναλυτικά οι μέθοδοι προσομοίωσης για την
αριθμητική προσέγγιση της πιθανότητας αστοχίας. Η
προσομοίωση Monte Carlo και η προσομοίωση με τη μέθοδο
των υποσυνόλων, εφαρμόζονται είτε με βάση την πραγματική
συνάρτηση αστοχίας είτε με βάση το μοντέλο kriging
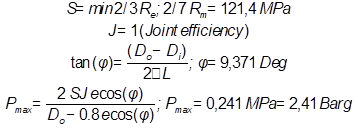 .
Οι δύο αυτές προσεγγίσεις παρουσιάζονται παράλληλα, ώστε
να φαίνεται η αντιστοιχία. Η κύρια διαφορά είναι ότι η
συνάρτηση πιθανοτικής ταξινόμησης π(x) αντικαθιστά το
δείκτη IF(x), όταν η προσομοίωση βασίζεται
στο μοντέλο kriging.
.
Οι δύο αυτές προσεγγίσεις παρουσιάζονται παράλληλα, ώστε
να φαίνεται η αντιστοιχία. Η κύρια διαφορά είναι ότι η
συνάρτηση πιθανοτικής ταξινόμησης π(x) αντικαθιστά το
δείκτη IF(x), όταν η προσομοίωση βασίζεται
στο μοντέλο kriging.
Στη συνέχεια, γίνεται λόγος για
τη χρήσιμη ιδιότητα της Importance Sampling (IS). Η IS
επιτρέπει την επιλογή διαφορετικής συνάρτησης συχνότητας
πιθανότητας (instrumental PDF), για την παραγωγή του
τυχαίου δείγματος στην εκτίμηση της πιθανότητας
αστοχίας. Με τη σωστή επιλογή εναλλακτικής ΣΣΠ, η
επαναληπτική διαδικασία της MCS μπορεί να επιταχυνθεί
σημαντικά. Επίσης αποδεικνύεται ποια είναι η βέλτιστη
ΣΣΠ, δηλαδή αυτή που μηδενίζει τη διακύμανση της
εκτιμώμενης πιθανότητας. Ωστόσο, η βέλτιστη ΣΣΠ απαιτεί
τη γνώση της πιθανότητας και συνεπώς είναι
μη-εφαρμόσιμη. Σε αυτό το σημείο παρουσιάζεται η νέα
υβριδική μέθοδος Meta-model based Importance Sampling
(MIS). Σκοπός της είναι η προσέγγιση της βέλτιστης ΣΣΠ
μέσω του μοντέλου kriging, και η παραγωγή περιορισμένου
τυχαίου δείγματος για την εκτίμηση της πιθανότητας. Με
άλλα λόγια, αν το μοντέλο kriging μπορεί να παρέχει μία
μέτρια έως καλή εκτίμηση της πιθανότητας αστοχίας, η MIS
διορθώνει σε δεύτερη φάση την πιθανότητα αστοχίας με
μικρό δείγμα που απαιτεί υπολογισμούς της συνάρτησης
αστοχίας. Η μέθοδος MIS συνδυάζει το μοντέλο kriging με
την Importance Sampling και είναι εξαιρετικά χρήσιμη
όταν απαιτείται επιβεβαίωση της εκτίμησης ή όταν το
μοντέλο είναι ανεπαρκές.
Το τρίτο κεφάλαιο περιλαμβάνει
τις στρατηγικές με τις οποίες η πρόβλεψη kriging μπορεί
να βελτιωθεί, ώστε να παρέχει πιο βέβαιη ταξινόμηση.
Όπως προαναφέρθηκε, η κατασκευή του μοντέλου βασίζεται
μονάχα σε ορισμένες παρατηρήσεις ή υποστηρικτικά σημεία,
τα οποία λαμβάνονται τυχαία από το πεδίο ορισμού της
συνάρτησης αστοχίας g(x) . Η βελτίωση του μοντέλου
επιτυγχάνεται λαμβάνοντας νέες παρατηρήσεις και
επανυπολογίζοντάς το. Τα νέα υποστηρικτικά σημεία
επιλέγονται, με βάση μία συνάρτηση-κριτήριο, που
λαμβάνει μεγάλες τιμές όταν η μέση τιμή μG(x)
πλησιάζει το μηδέν, και όταν η τυπική απόκλιση σG(x) αυξάνεται.
Με αυτόν τον τρόπο στοχεύονται οι περιοχές στις οποίες
γίνεται η μετάβαση από την αστοχία στην ασφάλεια και
αντίστροφα. Είναι οι περιοχές, δηλαδή, στις οποίες η
εκτίμηση της ταξινόμησης είναι πιο δύσκολη. Στην παρούσα
εργασία, δύο είναι τα κριτήρια στα οποία δίνεται
μεγαλύτερη έμφαση: Η συνάρτηση πιθανοτικού εύρους
(margin probability function MP(x) ) και η προτεινόμενη
συνάρτηση πιθανέστερης εσφαλμένης ταξινόμησης (most
probable misclassification function MF(x)). Στη
συνέχεια, τα άνω κριτήρια που κατευθύνουν στη μεταβατική
περιοχή της αστοχίας και της ασφάλειας,
πολλαπλασιάζονται με τη ΣΣΠ fX(x) του
προβλήματος αξιοπιστίας. Με αυτό τον τρόπο, το τελικό
κριτήριο fX(x)∙ MF(x) λαμβάνει επιπρόσθετα
υπόψιν ότι περιοχές με μεγάλες τιμές της ΣΣΠ είναι πιο
καθοριστικές στον υπολογισμό της πιθανότητας αστοχίας.
Σε αυτό το σημείο, το κριτήριο
για την επιλογή νέων παρατηρήσεων στην κατασκευή του
μοντέλου, χρησιμοποιείται ως ΣΣΠ για την παραγωγή
δείγματος. Το δείγμα αυτό είναι ένα σύνολο υποψήφιων
σημείων. Ωστόσο το μέγεθός του είναι μεγάλο και είναι
μη-αποδοτικό να επιλεγεί ολόκληρό. Προκειμένου να
επιλεγούν τα πιο αντιπροσωπευτικά σημεία, λύνεται το
πρόβλημα συσταδοποίησης (clustering problem) με τον
αλγόριθμο k-means. Έτσι το σύνολο των παρατηρήσεων
ανανεώνεται και το μοντέλο kriging είναι πιο ακριβές σε
κρίσιμες περιοχές.
Αντί της παραπάνω προσέγγισης,
δηλαδή της παραγωγής δείγματος με βάση την συνάρτηση
πυκνότητας πιθανότητας α fX(x)∙ MF(x) ,
προτείνεται, επιπρόσθετα, μία εναλλακτική λύση.
Δεδομένου ότι η διαδικασία ανανέωσης των παρατηρήσεων,
είναι μέρος ενός επαναληπτικού αλγορίθμου, και ότι η
πιθανότητα αστοχίας παρατηρείται σε κάθε βήμα, τότε
υπάρχει διαθέσιμο δείγμα που έχει παραχθεί από την
προσομοίωση MCS ή SS. Αυτό το δείγμα χρησιμοποιείται για
να λυθεί το πρόβλημα συσταδοποίησης, όμως κάθε σημείο
έχει διαφορετική βαρύτητα, που καθορίζεται από τη
συνάρτηση w(x)=MF(x). Με αυτόν τον τρόπο, αποφεύγεται η
παραγωγή δείγματος από την α fX(x)∙ MF(x),
που θα απαιτούσε δειγματοληψία από μαρκοβιανές αλυσίδες
και γίνεται περεταίρω εκμετάλλευση του υπάρχοντος
δείγματος από την προσομοίωση MCS ή SS.
Όπως προαναφέρθηκε, η διαδικασία
ανανέωσης των παρατηρήσεων γίνεται πολλές φορές
διαδοχικά με λίγα σημεία, ώστε το μοντέλο να μπορεί να
δίνει σε κάθε βήμα νέα κατεύθυνση. Το προτεινόμενο
κριτήριο για τη λήξη της διαδικασίας βασίζεται στην
ποσότητα pMF που ισούται με την ολοκλήρωση της
συνάρτησης fX(x)∙ MF(x) σε όλο το πεδίο
ορισμού. Αυτό επιτυγχάνεται με τον ίδιο τρόπο που
υπολογίζεται η πιθανότητα αστοχίας, και με το ίδιο
δείγμα. Αν, ιδανικά, το μοντέλο αποκτήσει τέλεια
ακρίβεια στην ταξινόμηση, η συνάρτηση MF(x) αποκτά
μηδενική τιμή, και συνεπώς μηδενίζεται το pMF
.
Στο τέταρτο κεφάλαιο, γίνεται
εφαρμογή της μεθόδου αξιοπιστίας που βασίζεται σε
μοντέλο kriging. Αυτή περιλαμβάνει την αρχική κατασκευή
του μοντέλου από τυχαία επιλεγμένες παρατηρήσεις, την
ανανέωση με νέα αποδοτικά υποστηρικτικά σημεία, την
τελική εκτίμηση της πιθανότητας αστοχίας, και την
επαλήθευση με την υβριδική μέθοδο Meta-model based
Importance Sampling. Τα προβλήματα στα οποία εφαρμόζεται
είναι προβλήματα με ανώμαλη (αλλά συνεχή) συνάρτηση
αστοχίας, πολλών διαστάσεων, και τα τελευταία δύο
αφορούν περιπτώσεις δομικής αξιοπιστίας. Το πρώτο είναι
ένα δικτύωμα μεγάλου ανοίγματος, με τυχαίες μεταβλητές
τα φορτία, τη γεωμετρία και τις ιδιότητες των υλικών,
στο οποίο μετράται η πιθανότητα υπέρβασης του
επιτρεπόμενου βέλους. Στο δεύτερο πρόβλημα, ένα κτίριο
ύψους 80 m προσομοιώνεται με την παραδοχή συνεχούς
καμπτοδιατμητικού προβόλου, με τυχαίες συνεχείς
μεταβλητές τη δυσκαμψία και την ανηγμένη καθ’ ύψος μάζα.
Επίσης, το φάσμα των επιταχύνσεων ακολουθεί
λογαριθμοκανονική κατανομή, όπως προκύπτει από
στατιστική επεξεργασία των Boore-Atkinson. Ως συνάρτηση
αστοχίας ορίζεται η υπέρβαση του drift κατά 0.75% .
Το τελευταίο κεφάλαιο
περιλαμβάνει τα τελικά συμπεράσματα. Η προσέγγιση των
προβλημάτων αξιοπιστίας των κατασκευών με τη γραμμική
πρόβλεψη kriging αποδεικνύεται αποδοτική, ειδικά σε
προβλήματα κάτω των 100 διαστάσεων, με συνεχή συνάρτηση
αστοχίας και μικρές πιθανότητες. Το μοντέλο kriging
μπορεί να επεκταθεί σε προβλήματα βελτιστοποίησης και σε
παλινδρόμηση μεγάλων δεδομένων (big data).