Υπάρχουν πλήθος δημοσιεύσεων στο αντικείμενο αυτό: Ο Rohde [1] το 1953 έδωσε μια λύση υπό την μορφή δυναμοσειράς στο πρόβλημα των μεγάλων μετατοπίσεων κολορουκωνικών πυλώνων.  Το 1968 ο Gaines και ο Voltera  [2] μελέτησαν τις ιδιοσυχνότητες τέτοιου είδους κατασκευών. Ο Wang και ο Lee [3] το 1973 συνέχισαν το έργο του Rohde [1] γενικεύοντας την λύση υπό την μορφή δυναμοσειράς.  Το 1975 ο Prathap και ο Varadan [4] παρουσίασαν τη μέθοδο των πεπερασμένων διαφορών για τέτοιους πυλώνες.  Ο Bouchet και ο Biswas [5] παρουσίασαν μια μη-γραμμική ανάλυση με χρήση της μεθόδου των πεπερασμένων στοιχείων, όπως επίσης και μια δυναμική ανάλυση το 1979. Ο Takabatake με διάφορους συνεργάτες του [6], [7], [8], [9] πρότεινε την λύση τέτοιων προβλημάτων με χρήση της συνάρτησης Dirac.  Θα πρέπει επίσης να αναφερθούμε στην μελέτη του Καθηγητού Ε.Μ.Π. Α. Κουνάδη [10] που αφορά την δυναμική απόκριση μιας δοκού εν προβόλω με συγκεντρωμένες μάζες, αλλά με σταθερή διατομή σε όλο το μήκος της.

2.  ΠΕΡΙΓΡΑΦΗ ΤΟΥ ΜΟΝΤΕΛΟΥ - ΑΝΑΛΥΣΗ

Το μοντέλο που μελετάμε είναι κατασκευασμένο από ομογενές ισότροπο υλικό με μέτρο ελαστικότητας Ε.  Η σχέση μεγέθους που συνδέει το μήκος του , την διάμετρό του στην βάση h και το πάχος της διατομής του είναι χαρακτηριστική για μια λεπτότοιχη ράβδο 

Η διατομή του πυλώνα μεταβάλλεται καθ΄ ύψος πράγμα που σημαίνει ότι και τα αδρανειακά χαρακατηριστικά της μεταβάλλονται συναρτήσει της αποστάσεως x της εκάστοτε διατομής από την βάση του πυλώνα, που θεωρούμε ως την αρχή του συστήματος συντεταγμένων (Σχ.1).  Κάθε ένα από αυτά τα χαρακτηριστικά είναι δυνατόν να εκφραστεί ως εξής:

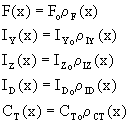
όπου    F       είναι το εμβαδόν της διατομής στην θέση x
            I_Y,Z    είναι οι ροπές αδρανείας της διατομής στην θέση x περί τους άξονες Υ και Ζ αντίστοιχα
            Ι_D        είναι η κατά S. Venant στρεπτική ροπή αδρανείας της διατομής 
            C_T     είναι η αντίσταση καμπύλωσης της διατομής

Οι συγκεντρωμένες αυτές μάζες αποτελούνται στην πράξη από πλάκες τοποθετημένες κάθετα στον άξονα ox του προβόλου όπως φαίνεται στο σχήμα 1:

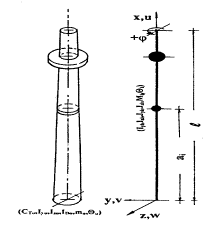
Σχ. 1

Η διπλωματική εργασία μελετά σε πρώτη φάση την επιρροή της στροφικής αδράνειας των μαζών αυτών περί τους άξονες Υ, Ζ στην δυναμική απόκριση της κατασκευής, πράγμα το οποίο μέχρι σήμερα παραλείπεται, μη λαμβάνοντας υπόψη την διαφραγματική λειτουργία των μαζών αυτών. Στη συνέχεια εξετάζεται η επιρροή και της διαφραγματικής λειτουργίας των μαζών, πράγμα το οποίον επίσης παρελείπετο μέχρι τώρα.

Μελετάται αρχικά η ελεύθερη ταλάντωση μιας τέτοιας κατασκευής κάνοντας χρήση της μεθόδου Galerkin και των ιδιομορφών του απλού προβόλου (χωρίς συγκεντρωμένες μάζες) με σταθερή διατομή. Στη συνέχεια επιλύεται το πρόβλημα της εξαναγκασμένης κίνησης  τόσο της καμπτικής όσο και της στρεπτικής ταλάντωσης με την χρήση του μετασχηματισμού Carson – Laplace υπό δυναμικά φορτία. Δίδονται τέλος οι ιδιαίτερες σχέσεις που ισχύουν για την περίπτωση των φορτίσεων ανέμου και σεισμού.

 3.   ΑΡΙΘΜΗΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ

Μελετώνται αρχικά δύο (2) πυλώνες με δύο συγκεντρωμένες μάζες έκαστος. Υπολογίζονται οι καμπτικές ιδιοσυχνότητες, οι συναρτήσεις σχήματος και οι παραμορφώσεις τους λόγω ανεμοπιέσεως όπως επίσης και  λόγω σεισμικών φορτίων.

Οι ίδιοι πυλώνες αλλά μη λαμβάνοντας υπ’ όψη την στροφική αδράνεια των συγκεντρωμένων μαζών εξετάζονται για τα ίδια εξωτερικά φορτία και μελετάτε η επιρροή της στροφικής αδρανείας τους.

Στη συνέχεια εξετάζονται τεσσερις (4) πυλώνες με δύο συγκεντρωμένες μάζες έκαστος και γίνεται σύγκριση των τριών πρώτων καμπτικών ιδιοσυχνοτήτων τους για τις εξής περιπτώσεις:

(Α) Χωρίς συγκεντρωμένες μάζες
(Β) Με συγκεντρωμένες μάζες χωρίς όμως στρεπτική ακαμψία
(Γ) Με συγκεντρωμένες μάζες και στρεπτική ακαμψία